Difference between revisions of "Curvature"
Jump to navigation
Jump to search
| Line 21: | Line 21: | ||
* the curvature at each point is estimated by best fitting a quadric around it | * the curvature at each point is estimated by best fitting a quadric around it | ||
* if there's not enough neighbors to compute a quadric (i.e. less than 6) an invalid scalar value (''NaN'') is set for this point. This point will appear in grey (or not at all if you uncheck the 'display NaN values in grey' option of the scalar field parameters). | * if there's not enough neighbors to compute a quadric (i.e. less than 6) an invalid scalar value (''NaN'') is set for this point. This point will appear in grey (or not at all if you uncheck the 'display NaN values in grey' option of the scalar field parameters). | ||
| + | * the reference articles for the computation of the Mean and Gaussian curvatures are: | ||
| + | ** "CURVATURE OF CURVES AND SURFACES – A PARABOLIC APPROACH", Zvi Har'el (1995) - ''for the formulas to compute the curvature values'' | ||
| + | ** "THREE-DIMENSIONAL SURFACE CURVATURE ESTIMATION USING QUADRIC SURFACE PATCHES", I. Douros & B. Buxton, University College London (2002) - ''for the fitting of the 3D quadric on the points'' | ||
| + | * the computation of the 'Normal change rate' curvature is derived from the PCL library implementation (it's equal to the samllest eigenvalue divided by the sum of the 3 eigenvalues of the local cloud covariance matrix - see [https://pointclouds.org/documentation/classpcl_1_1_normal_estimation.html#a81b73d67bfdb2d70e09d8b2cd4749f45 pcl::NormalEstimation::computePointNormal]). | ||
Revision as of 03:21, 10 January 2022
Menu
This tool is accessible via the 'Tools > Other > Curvature' menu.
Description
This tool evaluates the curvature of a point cloud.
Procedure
Select one or several point clouds then start this tool.
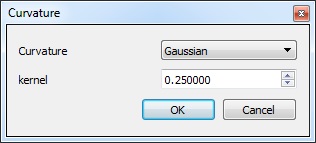
A dialog will appear:
Parameters
- Curvature: choose the curvature type (Mean, Gaussian or the simpler 'Normal change rate' )
- kernel: neighborhood size (for quadric fitting - see Notes below)
Notes:
- the curvature at each point is estimated by best fitting a quadric around it
- if there's not enough neighbors to compute a quadric (i.e. less than 6) an invalid scalar value (NaN) is set for this point. This point will appear in grey (or not at all if you uncheck the 'display NaN values in grey' option of the scalar field parameters).
- the reference articles for the computation of the Mean and Gaussian curvatures are:
- "CURVATURE OF CURVES AND SURFACES – A PARABOLIC APPROACH", Zvi Har'el (1995) - for the formulas to compute the curvature values
- "THREE-DIMENSIONAL SURFACE CURVATURE ESTIMATION USING QUADRIC SURFACE PATCHES", I. Douros & B. Buxton, University College London (2002) - for the fitting of the 3D quadric on the points
- the computation of the 'Normal change rate' curvature is derived from the PCL library implementation (it's equal to the samllest eigenvalue divided by the sum of the 3 eigenvalues of the local cloud covariance matrix - see pcl::NormalEstimation::computePointNormal).